Inhaltsverzeichnis
In diversen Handwerks-, Bau- und Produktionsbetrieben wird die Hebelwirkung genutzt, um mit Hebeln wie Brechstangen, Schraubenschlüsseln oder Kransystemen verschiedene Montage- und Bauarbeiten sowie den Lastentransport zu vereinfachen. Hebeleffekte dienen außerdem der Kraftübersetzung an Maschinen. Betriebsinterne Arbeitsabläufe können so sicher und komfortabel durchgeführt werden. Dazu müssen die verschiedenen Kräfte am Hebel mithilfe von Formeln berechnet werden.
Das Hebelgesetz als Grundlage für die Hebelberechnung
Ein Hebel wird in der Physik und in der Technik als sogenannter Kraftwandler bezeichnet: Der starre Hebelkörper ist um seine eigene Achse herum – vergleichbar mit einer Wippe – drehbar. Das Hebelgesetz berücksichtigt dazu einseitige und auch zweiseitige Hebel. Der Hebeleffekt beziehungsweise die Hebelwirkung macht es möglich – auch mit einem geringen Kraftaufwand – schwere Lasten anzuheben und zu bewegen.
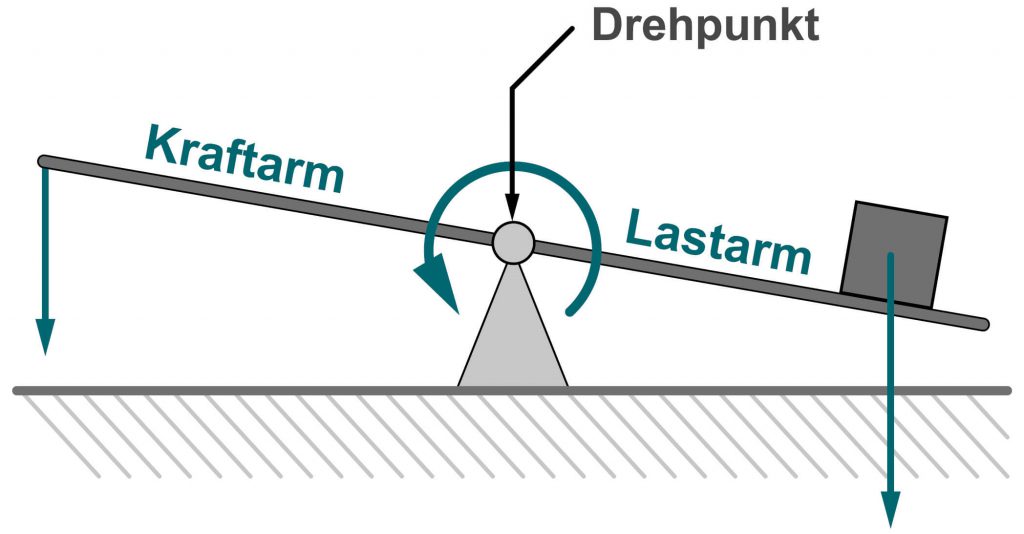
Die Hebelkraft wird über das Hebelgesetz definiert und berechnet. Das aus der Antike stammende Gesetz kann für das obige Beispiel mit folgender Formel zunächst einfach ausgedrückt werden:
F1 × d1 = m × g × d2
Der Lastarm bezeichnet hierbei die Seite, an der sich die zu bewegende Last befindet. Der Kraftarm definiert die Seite, an der die bewegende Kraft anliegt. Der so genannte Dreh- oder Angelpunkt ist jener Punkt, um den sich der Hebel drehen lässt. Das Drehmoment ist definiert als
M = F x d
Hierbei gilt: Je länger der Hebel d ist, desto größer ist das Drehmoment M.
Den Hebel bei ein- und zweiseitigen Hebeln berechnen
Obwohl die Berechnungsformel für ein- und zweiseitige Hebel dieselbe ist, wird in der Theorie zwischen diesen beiden Hebelformen unterschieden.
| Hebel | Merkmale |
|---|---|
| einseitiger Hebel | Last- und Kraftarm fallen zusammen, d. h. die Hebelkräfte greifen nur an einer Seite des Drehpunktsder Drehpunkt befindet sich an einem Ende des Hebelarms (außerhalb der beiden Kräfte)die Kräfte wirken in eine Richtung |
| zweiseitiger Hebel | die Kraftangriffspunkte liegen auf beiden Seiten des Drehpunkts die Kräfte wirken in zwei Richtungen |
Beispielrechnung:
Als Beispiel für einen Hebel dient eine Schubkarre, mit der eine Last von 100 kg transportiert werden soll. Durch Umstellung der Formel
F1 × r1 = m × g × r2
zu F1
F1 = F2 × (r2/r1)
(dadurch wird F1 kleiner, je länger die Griffe der Schubkarre sind)
und r2 = 0,6 m und r1 = 1,8 m, gilt:
F1 = 100 kg x 9,81 m/s² x 0,6 m / 1,8 m = 327 N
9,81 m/s² ist die Erdbeschleunigung. 327 N sind die Kraft, die benötigt wird, um 327 N/9,81 m/s² = 33,33 kg zu heben.
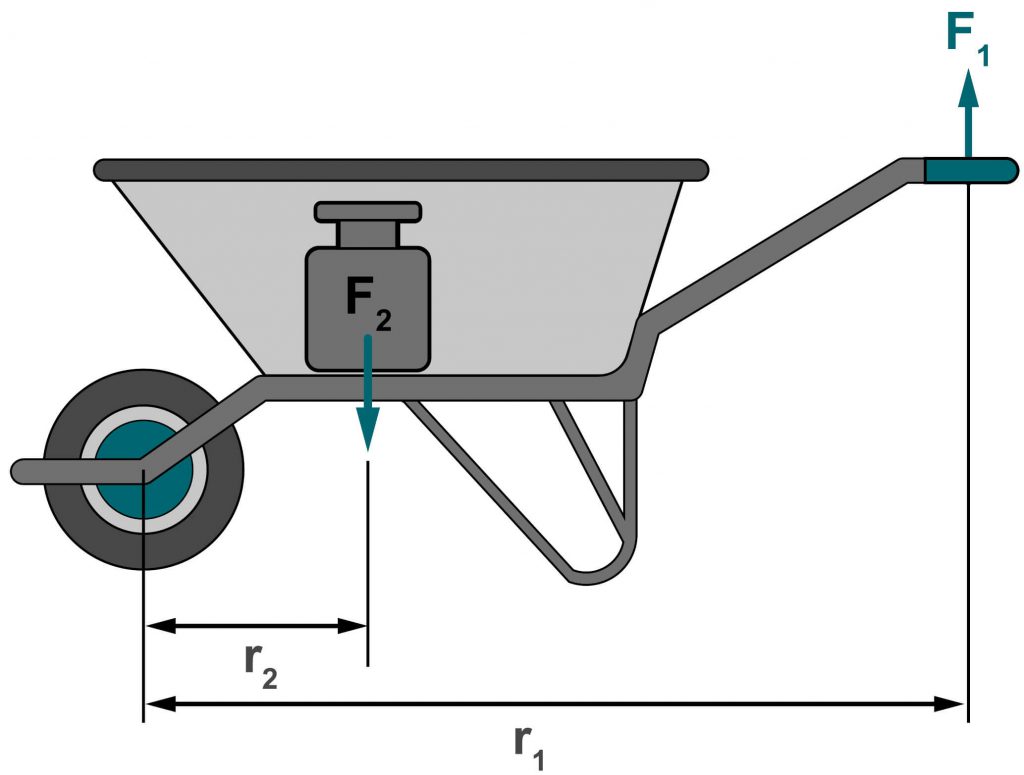
Die Schubkarre und der Hebeleffekt reduzieren die benötigte Kraft also um ein Drittel. Oder anders ausgedrückt: Über die Hebelwirkung kann am zweiten Kraftarm 5-mal so viel Kraft erzeugt werden. Die Formel für die Berechnung des Hebels an zweiseitigen Hebeln kann auch für einseitige Hebel angewendet werden: Müssen Sie z. B. eine beladene Schubkarre bewegen, so wirken zwar beide Kräfte nur auf einer Seite, durch die geladene Last ergeben sich aber zwei Hebelarme mit unterschiedlicher Länge.
Sind Hebel nicht als gerader Körper ausgebildet, so spricht man auch von geknickten Hebeln oder Winkelhebeln. Letztere finden etwa in der Neigungswaage ihre Anwendung. Bei allen Hebelarten muss zusätzlich zur Kraft noch die Reibung im Drehpunkt berücksichtigt werden: Wird der Hebel über der Achse gedreht, wird ein Teil der aufgewendeten Energie in Wärme umgewandelt. Zur benötigten Hebelkraft ist also ein Kraftaufwandszuschlag je nach Hebelmaterial und Last nötig.
Hebezeuge: praktische Nutzung von Hebeln im Betrieb
Viele Hebezeuge nutzen den Hebeleffekt, der im Hebelgesetz beschrieben wird und verringern so den Kraftaufwand beim Anheben und Bewegen schwerer Lasten. Zu ihnen zählen sowohl manuell betriebene als auch elektro-hydraulische Hubsysteme und Hebezeuge mit und ohne Neigungsfunktion. Sie finden sich in der Logistik ebenso wie auf Baustellen wieder und verbinden eine hohe Tragkraft mit einer einfachen und komfortablen Handhabung. Typische Hebezeuge im Betrieb sind etwa:
- Hebel- und Handkettenzüge
- Kransysteme
- Materiallifter
- Hebegeräte
- Niveaulifter
- Elektrokettenzüge
Die Hebezeuge stellen aufgrund ihrer großen Kraftübersetzung dauerhaft eine Arbeitserleichterung in vielen betrieblichen Bereichen dar: Sie tragen zu effektiven und sicheren Arbeitsabläufen bei und erhöhen die Umschlaggeschwindigkeit in Lager und Produktion. Zudem lassen sich die Betriebskosten durch den Einsatz dieser hochwertigen Arbeitsmittel in vielen Fällen deutlich verringern.
FAQ zum Hebel berechnen
Ein Hebel wird in der Physik und in der Technik als sogenannter Kraftwandler bezeichnet: Der starre Hebelkörper ist um seine eigene Achse herum – vergleichbar mit einer Wippe – drehbar. Das Hebelgesetz berücksichtigt dazu einseitige und auch zweiseitige Hebel. Der Hebeleffekt beziehungsweise die Hebelwirkung macht es möglich – auch mit einem geringen Kraftaufwand – schwere Lasten anzuheben und zu bewegen.
Nach dem Hebelgesetz kann die Hebelkraft bei einseitigen Hebeln mit Zusatzgewicht sowie zweiseitigen Hebeln mit dieser Formel berechnet werden:
F1 x r1 = F2 x r2
Hebel werden in ein- und zweiseitige Hebel unterschieden. Einseitige Hebel sind dadurch gekennzeichnet, dass:
• Last- und Kraftarm zusammenfallen, d. h. die Hebelkräfte greifen nur an einer Seite des Drehpunkts
• der Drehpunkt sich an einem Ende des Hebelarms befindet
• die Kräfte in eine Richtung wirken
Zweiseitige Hebel zeichnen sich wiederum dadurch aus, dass sie:
• die Kraftangriffspunkte auf beiden Seiten des Drehpunkts liegen
• die Kräfte in zwei Richtungen wirken
Bildquelle:
© gettyimages.de – PRImageFactory
























